One primary requirement of environmental risk assessment and management is the ability to analyze and predict the transport of toxins (Thomann 1989). Other requirements include evaluation of the stochastic behavior of toxins in the water, sediments, and organisms. There are two main types of models of toxin fate in aquatic systems: steady-state models and time-variable models. Steady-state models are useful for determining the basic principles of the fate of a toxin and its uptake into the food web. Such models make several simplifying assumptions, the most significant being the assumption of no variation in toxin concentration. Time-variable models, on the other hand, are more useful for predicting recovery times after some program of toxin control.

Sampling from a bridge. By sampling during the outgoing (flow to left) and ingoing tide it is possible to collect water and particles, in order to establish a budget of particle, water, and cadmium exchange through this main entrance to East Foundry Cove.

A basic steady-state model assumes a 1 dimensional river into which a toxin is added at one point in time (see Figure 1). The toxin is assumed to exist in two forms: dissolved and particulate (i.e., the toxin sorbed onto particulate matter). Mass balance equations summarize the fate of the toxin by incorporating all mechanisms of input and loss of the toxin into separate equations for the water column, surface sediment, and deeper sediments. These equations are mathematically complex because they incorporate many terms for complex processes such as particulate settling, resuspension, burial, diffusive exchange between layers, as well as volatilization and biodegradation (Thomann 1989). A typical mass balance equation (for a dissolved toxin in the water column) models the change () in toxin concentration (cd) over time (t) as a function of all input, transfer, and loss mechanisms:
cd / t = [transport + dispersion] + [sorption – desorption] +
[sediment diffusive exchange] – [decay + losses] –
[volatilization] + [input]
Decay and loss include mechanisms such as biodegradation and photolysis. Input includes all point discharge sources as well as nonpoint and tributary inputs. Separate equations are written for the toxin (in dissolved and particulate form) in the water column and sediment layers. Mass balance equations for sediments include additional terms for diffusion of the toxin between surface and deeper sediments and burial of the toxin. Similar equations can be written for the particulate form of a toxin with the addition of particulate settling and resuspension terms:
cp / t = [transport] – [desorption – sorption] -[particulate settling] + [particulate resuspension] – [decay] + [input]
Estimation of these individual parameters is not trivial. In addition to these physical and chemical parameters, the transfer of the toxin through the food chain by direct uptake from the water column and by the consumption of contaminated prey must also be included in models for a complete understanding of the fate of a toxin in an ecosystem.
A simple approach can be taken when all material is passing past a small cross-section of the river. Nearly all Foundry Cove tidal flow passes under a narrow railroad bridge. This allows us to sample water on the outgoing and incoming tide and to analyze Cd dissolved in water and sorbed onto particles. As it turns out, nearly all the Cd was found on the particles trapped on a filter and only trivial amounts were found in the water column (see Figure 2). There was a net transport of Cd on particles from within Foundry Cove to the main stem of the Hudson River. This is a bit shaky , but if we extrapolate data from just a couple of tidal cycles to the whole year , we estimate that, in 1993, approximately 0.5 -1 MT of Cd were being exported from Foundry Cove to the main stem of the Hudson.
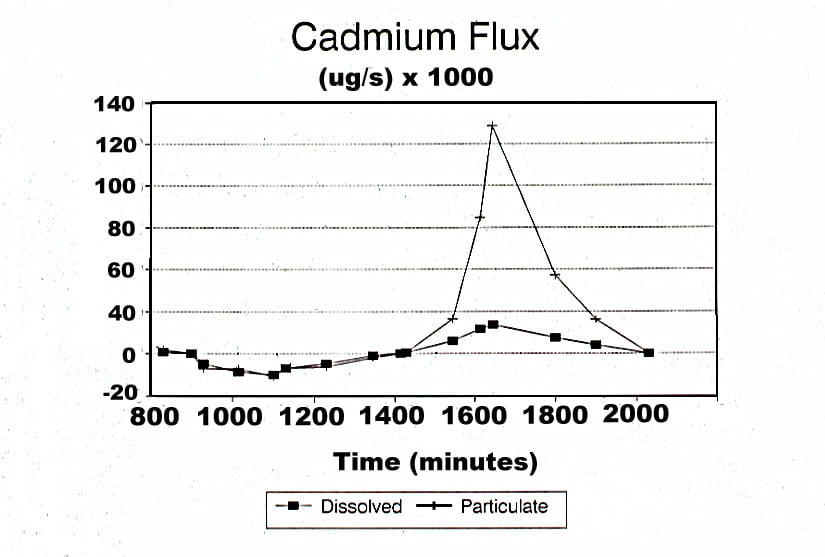
Cadmium flux to and from East Foundry Cove in the water and on particles. A positive value indicates export from E. Foundry Cove to the main part of the Hudson River. Note that most material is moving on particles (data collected by Randy Young)
