Fair warning: This will be surprisingly simple.
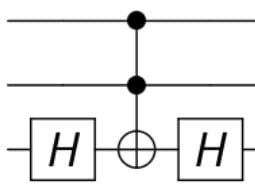
Since you understand the 2-qubit Grover’s Algorithm now, it’s quite easy to scale up to 3-qubits. Firstly, regarding the oracle, there is a CCZ gate which has a matrix \(\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 \\
\end{bmatrix}\) which already marks \(|111\rangle\) with a negative just like that. And using the same idea from last time, we can manipulate what it marks using X gates before and after the CCZ gate. By the way, in Jupyter, a CCZ gate is created with two Hadamard gates, one on each side of the target qubit, and a Toffoli gate (CCNOT).
Also, for reference, the columns and rows essentially just increase in binary all the way to \(111\). They start at \(000\), then \(001\), then \(010\), \(011\)…
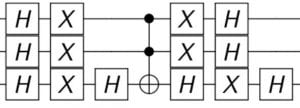
So now that the oracle is completed, we just need to be able to reflect the amplitude which is also surprisingly easy as we already have a general formula \(H^{\otimes n}(2|0\rangle\langle 0|-I)H^{\otimes n}\) which we can accomplish with this circuit:
Jupyter has no formatting method for circuit drawing so here is a neater visual that I drew:
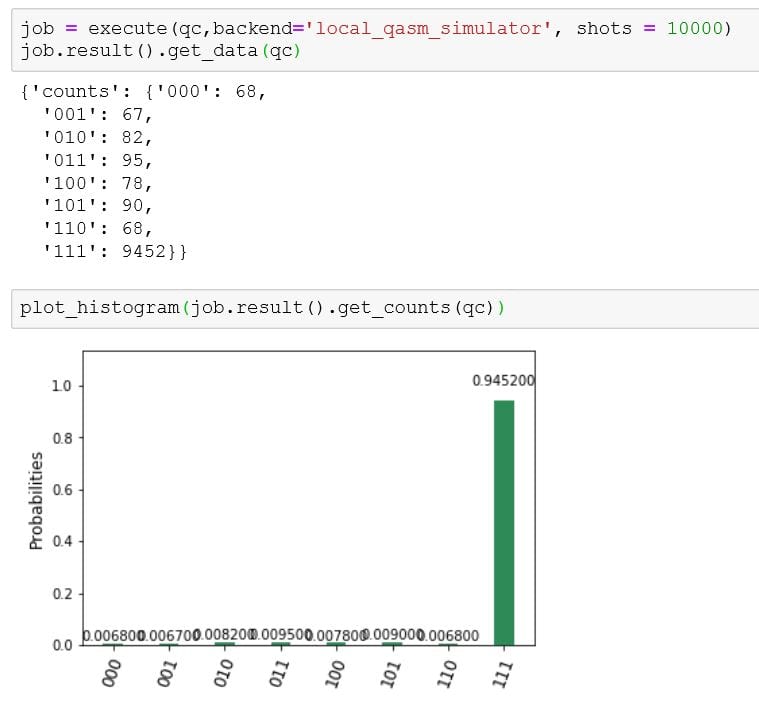
Don’t forget that we need to calculate how many times to run Grover’s iteration though. Using the formula $$sin(\theta) = \frac{2\sqrt{M(N-M)}}{N}$$ with \(M = 1\) and \(N = 2^3 = 8\), we can easily calculate \(\theta\) to be \(41.41^\circ\) and thus the starting angle to be \(20.7^\circ\). Clearly, with two rotations, we get the closest to \(\frac{\pi}{2} radians = 90^\circ\) even though we rotate slightly past it. This also falls in line with the other formula $$R \leq \lceil\frac{\pi}{4}\sqrt{\frac{N}{M}}\rceil$$ in which we can calculate R to be 3. Thus, at most 3 rotations are required to get close to \(|\beta\rangle\) and we calculated the exact number to be 2.
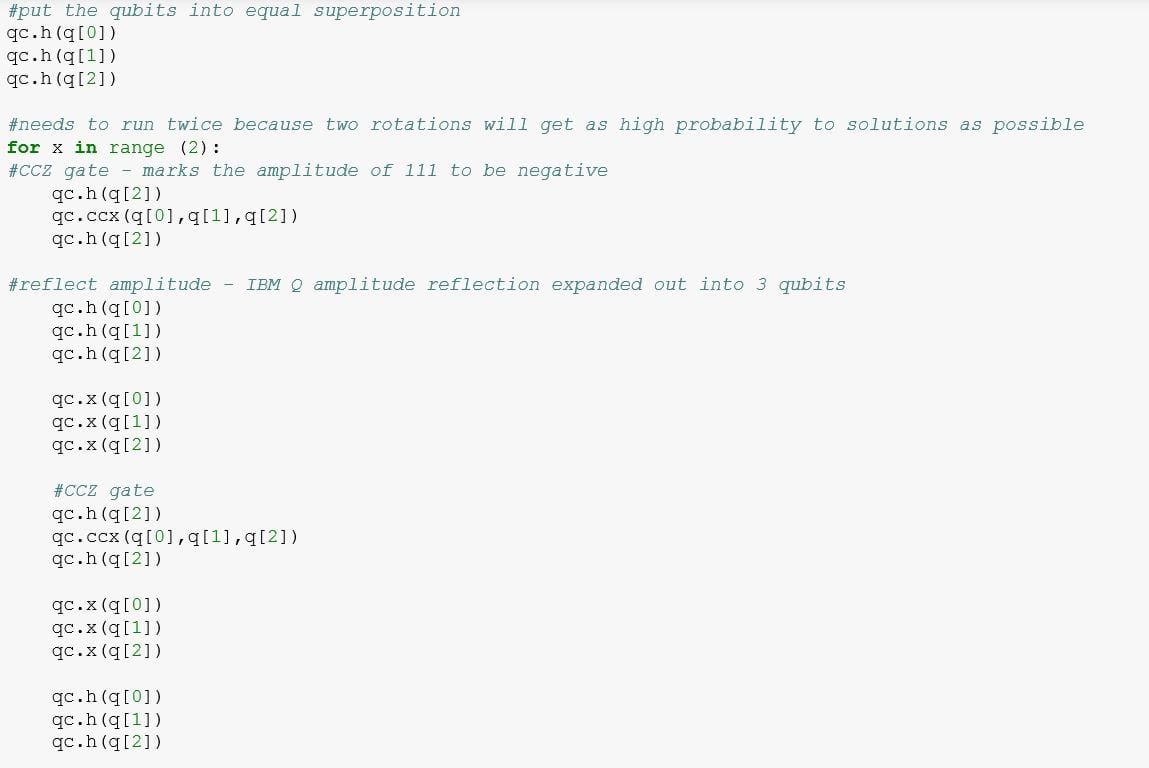
You can try this out for yourself in Jupyter. I included my code and my drawn circuit down below:
Keep in mind, this 3-qubit form of Grover’s algorithm is so easy precisely because a CCZ gate exists. For four qubits, there is no CCCZ gate and thus is considerably more complex.


Thanks for your nice example of Grover’s algorithm. I noted that changing the oracle to specify |101> instead of |111> gave better result after one rotation than two! So, the formula used above to find the number of rotations should be handled with care it seems.
Hi Robert, would you be so kind and tell us your layout (maybe in IBM composer) for Grover’s algorithm for 3 QuBits where the oracle specifys |101> ?
Hi Oliver, the trick is to identify the “Grover diffusor” as this, together with the oracle are the parts that are repeated at each iteration. The diffuser consists of the following sequence of operations: D = H1, H2, H3, CPS, H1, H2, H3
where Hn indicates Hadamard applied to qubit n. CPS is “conditional phase shift”, meaning that the sign is reversed of all coefficients except the one at the origin.
The oracle is the operation that defines which coefficient has opposite sign to all other coefficients (given an input uniform state):
E.g. an oracle that produces |101> could look like: O = H3, CCNOT3, H3, CCNOT2.
So a two-iteration algorithm would then become: Grover = O, D, O, D
I am sorry that I am not able to express this in IBM composer code as I am using home-made python code when I test these things. Hope that is is clear though!
A correction: I have identified that my oracle for |101> that is shown above is faulty. Instead O = H2, CCZ (control_control_Z), H2 is the correct oracle. My former oracle works fine when all the input amplitudes are equal but not otherwise.
Using the new oracle results in an improvement also after a second rotation.
Thanks Oliver for pointing this out!
Excellent information, very functional and interesting for me. Thanks for sharing. Calculator