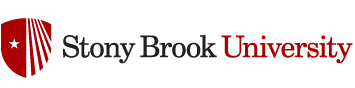General Background
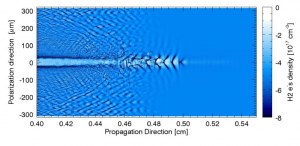
Plasma based accelerators sustain accelerating fields that surpass the typical RF cavity breakdown limitations by several orders of magnitude, and are able to accelerate leptons to higher energies in much shorter distances [1]. In particular, in the nonlinear blowout regime of the Plasma Wakefield Accelerator (PWFA), an intense laser pulse or an ultra-relativistic particle bunch propagates through a plasma containing free electrons and ions. This drive pulse radially expels the plasma electrons, and generates a cavity that consists only of the remaining ions. The space charge of the cavity ions is responsible for attracting electrons towards the propagation axis, giving the cavity a bubble like structure (see Fig. 1 below). An electron bunch at the back of this cavity will experience accelerating forces that scale with the plasma background density, and can exceed 100 GeV/m. Numerical simulations along with experiments have played a critical role in the many breakthroughs and advances of PWFAs. Nevertheless, further research into the processes is required for obtaining collider-quality beams, which are very challenging to model analytically.
Figure 1 – 3D Illustration of the blowout regime of the Plasma Wakefield Accelerator. The laser pulse / particle beam is represented by the red sphere and propagates, in the direction of the red arrow, into an uniform plasma of electrons with density isosurfaces in blue (lighter corresponding to very low concentration of electrons). The 2D plane projections show the integrated charge density of the pulse/ beam (red) and electrons (blue) in the direction normal to it.
Research with SLAC
The experiments at FACET-I showed groundbreaking results for lepton beam acceleration in plasma wakefields [2-6]. In [6] the 20GeV, 3nC and 13kA electron beam available at FACET-I was shown to drive a nonlinear plasma wake like the one described above. The configuration used allowed for the localized injection of electrons, resulting from the ionization of plasma impurity atoms. As a result, injected electrons were accelerated up to 30 GeV, had a final energy spread of only 10% and formed a bunch with emittance one order of magnitude below the drive beam. The next generation facility, FACET-II, aims to deliver a 10 GeV, 2nC and peak current reaching over 70kA electron beam. We intend to use that beam to explore the technique used in [6] to produce collider quality injected electron bunches. Analytically modeling the nonlinear wakefields and ionization injection acceleration process is a very complex and challenging endeavor. Therefore, we will resort to numerical simulations to determine the optimal beam and plasma parameters to demonstrate the injection and acceleration of collider quality electron beams once FACET-II becomes commissioned. Figure 2 shows initial 2D-cylindrical geometry (r,z) simulation results for this test case.
Figure 2 – Sample output from 2D-cylindrical OSIRIS simulation where the FACET-II inspired electron beam (in red) was sent into a pre-formed Hydrogen plasma (in blue) with 1% impurity of Helium. The Helium ionized electrons (in green) are injected locally at the back of the bubble where the wakefields both accelerate and focus them. Propagation direction goes to the right side of the plot. Color scales show electron densities.
Research with Brookhaven National Laboratory
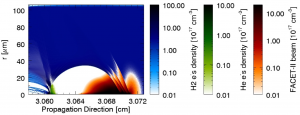
The ATF facility provides a 1TW, 3.5ps long 10.6µm wavelength CO2 laser pulse capable of driving plasma wakes. Our main goal is to investigate the wake structures using a long electron beam to transversely probe the wakefield, similarly to the method applied in [7]. At the moment we are assembling the plasma chamber that will allow for a wide range of experimental parameters such as plasma densities and profiles, to be studied. The available long laser pulse, however, will not drive the PWFA in the blowout regime. Instead, its envelope will undergo modulations due to the effect of the plasma density fluctuations in the local index of refraction. The self-modulated laser pulse can be interpreted as a sequence of short laser pulses distanced of the plasma period that resonantly excite plasma wakefields. At the back of the ATF long pulse the wakefields become large enough to expel the plasma ions and the laser starts to generate a hollow channel, depleted of both electrons and ions [8]. Figure 3 plots the plasma electron density as the self-modulated laser excites the wakes and creates the channel.
Figure 3 – Result of a 2D cartesian OSIRIS simulation where the ATF inspired CO2 laser pulse (not shown) was sent into a pre-formed Hydrogen plasma (density scale in blue) and excited wakefields that resonantly increase throughout the pulse until they are capable of repelling both electrons and ions, thus forming a hollow channel (region below x1 = 0.45). Propagation direction goes to the right side of the plot. Even though the important physics occur at the center (transversely) of the box, the large range of interactions necessitates a wide simulation box.
Plasma electrons that are trapped within the channel will perform betatron oscillations due to the transverse fields and will be subject to the direct laser acceleration mechanism [9]. As a consequence, they will emit hard-xray radiation suitable for applications in medicine, industry and material science [10]. Numerical studies are vital to investigate the plasma density, field structures, acceleration and radiation mechanisms in these scenarios. Additional simulations will be required to follow the potential path of the ATF laser power upgrades in the near future after which the plasma wake can be excited in the nonlinear blowout regime where the intense wakefields can accelerate particles efficiently over long distances [2,3].
Research with Laboratory for Laser Energetics (LLE)
Flying Focus [11] is a method invented by our LLE collaborators whereby a hyperchromatic lens is used in conjunction with a chirped pulse to create an ionization wave. The velocity, shape and the direction of propagation of this wave may be controlled by the spatial and temporal properties of the incoming laser pulse. This method represents a very promising avenue for generating meter-scale plasma columns as the basis of a plasma wakefield accelerator.
Current research consists of exploring the properties of the generated plasma column in theory and simulations as a function of the laser properties. Experimental verification of these results will be pursued for proof-of-principle laser parameters, potentially using the Multi-TeraWatt (MTW) laser at LLE
[1] – E. Esarey, et al., Rev. Mod. Phys., 81 1229-1285 (2009) [2] – I. Blumenfeld, et al. Nature, 445, 741-744 (2007) [3] – M. Litos, et al. Nature, 515, 7525, 92-95 (2014) [4] – S. Gessner, et al., Nature Communications, 11785, doi:10.1038/ncomms11785 (2016) [5] – S. Corde, Nature, 524, 442–445, doi:10.1038/nature14890 (2015) [6] – N. Vafaei-Najafabadi, et al. AIP Conf.Proc., 1777 (2016) 070011 [7] – C. J. Zhang, et al., Nature Sci. Rep. 6: 29485, doi: 10.1038/srep29485 (2016) [8] – N. Lemos et al., Plasma Phys. Controlled Fusion, 58, 3:034018, doi: doi: 10.1088/0741-3335/58/3/034018(2016) [9] – J. Shaw, et al., Phys. Rev. Lett., 118, 064801 (2017) [10] – F. Albert and A. G. R. Thomas, Plasma Phys. Controlled Fusion, 58, 10 : 103001, doi: 10.1088/0741-3335/58/10/103001 (2016) [11]- D. H. Froula, et al., Nature Photonics 12, 262-265 (2018).